MM Dataverse

Programming မှာ တွေ့ရတတ်တဲ့ Logical Operators တွေနဲ့ Boolean Data Types တွေ ဖြစ်တဲ့ 1 , 0 ( True, False) တို့ဟာ Boolean  Algebra ရဲ့ သဘောတရားတွေကို အသုံးချထားတာ ဖြစ်ပါတယ်။ 

ဒီနေ့မှာတော့ Boolean Algebra နဲ့ ပက်သက်ပြီး ကျွန်တော်တို့ Myanmar Dataverse Page ကနေ အနည်းငယ် ဖော်ပြပေးပါမယ်။ 

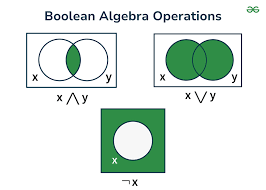
Brief History of Boolean Algebra and Programming

Boolean Algebra ကို ၁၈၅၄ ခုနှစ်မှာ  George Boole ဆိုတဲ့လူက စတင် တီထွင်ခဲ့တာပါ။ George Boole က ဒီ Boolean Algebra သဘောတရားတွေနဲ့ ပက်သက်ပြီး သူ့ရဲ့ “ The laws of thoughts” စာအုပ်မှာ စတင်ဖော်ပြခဲ့ပါတယ်။ 

ဒီ Boolean Algebra ဆိုတာက Electronic နဲ့ Computing ပိုင်းမှာ အသုံးပြုလို့ရတယ်ဆိုတာကို ( The Father of Information Theory လို့ မှတ်တမ်းတင်ခံရတဲ့ ) Claude Shannon ဆိုတဲ့ အမရိကန် က သင်္ချာပညာရှင်ဆိုသူက ထုတ်ဖော်လာပါတယ်။  

၁၉၃၇ ခုနှစ်မှာ Shannon ဟာ MIT မှာ “ A Symbolic Analysis of Relay and Switching Circuits “ ဆိုတဲ့ Master’s Thesis (မဟာသုတေသနစာတမ်း) တစ်ခုကို ရေးသားခဲ့ပြီ: အဲဒီစာတမ်းက Boolean Algebra ကို Digital Systemတွေမှာ အသုံးပြုနိုင်ဖို့ အခြေခံကျတဲ့ အကြောင်းအရာတွေကို ဖော်ပြခဲ့ပါတယ်။  

၁၉၄၀ နောက်ပိုင်းမှာ machine code နဲ့  Assembly Language စနစ်တွေ စတင်ထွန်းကားလာကာ ၁၉၄၀  ပြည့်နှစ်နဲ့ ၁၉၅၀ ပြည့်နှစ်တွေကြားမှာ ENIAC, EDVAC, UNIVAC စတဲ့ ပထမဆုံး ကွန်ပျူတာစနစ်တွေ ဖွံ့ဖြိုးလာခဲ့ပါတယ်။ ဒီစနစ်တွေမှာ Boolean Algebra နဲ့ Logic Circuits တွေကို အသုံးပြုထားပါတယ်။  

၁၉၅၈ ခုနှစ်မှာ Jack Kilby နဲ့ Robert Noyce တို့က  ကျွန်တော်တို့ ဆယ်တန်းတုန်းက Modern Physics မှာ သင်ဖူးတဲ့ Integrated Circuit (IC) တွေကို တီထွင်ခဲ့ပြီး၊ ဒီ IC တွေဟာ Boolean Algebra ရဲ့ သဘောတရားတွေကို အခြေခံထားပြီး၊ Logic Gates တွေကို တစ်စုတစ်စည်းတည်းအဖြစ် ထည့်သွင်းထားပါတယ်။ 

1970 နောက်ပိုင်းမှာတော့ Programming တွေ Personal  Computer တွေ Electronic စနစ်တွေ  တောက်လျှောက်တိုးတက်လာပြီး Boolean Algebra ရဲ့ သဘောတရားတွေကို အသုံးပြုပြီး ကျွန်တော်တို့တွေ Programm တွေရေးနေကြတဲ့ အထိ ဖြစ်လာပါတယ်။ 

Addition Rule and Multiplication Rule

ကျွန်တော်တို့ maths မှာ ဆိုရင် 0 နဲ့ ပက်သက်ပြီး + , x စတဲ့ Operator နှစ်မျိုးနဲ့ မှာ အခြေအနေ နှစ်ခုရှိပါတယ်။ Logical ပိုင်းတွက်ချက်ဖို့ အတွက်ဆို Addition Rules တွေထဲက တစ်ခုနဲ့ Multiplication Rules တွေထဲက တစ်ခုကို အသုံးပြုရပါတယ်။

Addition Rule

• 0 နဲ့ number တစ်ခုခု ပေါင်းရင် ပေါင်းတဲ့ number ပြန်ရပါတယ်။ ( 0+x = x)

Multiplication Rule

• 0 နဲ့ number တစ်ခုခု မြှောက်ရင် ပေါင်းတဲ့ 0 ပဲ ရပါတယ်။ ( 0*x = 0)

Dependent and Independent Events (And ဆိုမြှောက် Or ဆို ပေါင်း Not ဆိုပြောင်းပြန်  )

အခြေအနေ နှစ်ခု နဲ့ Probability ရဲ့ event နှစ်ခု ရှိတယ်။ အဲ့ Event နှစ်ခုကနေ အခြား event တစ်ခုရဲ့ Probability ကိုသိချင်တဲ့ အခါ အရင် Event နှစ်ခု Probability နှစ်ခု Dependent or Independent ပေါ်မူတည်ပြီး Output ကကွာခြားပါတယ်။ အဲ့ event တွေနဲ့ Logical operators တွေ အလုပ်လုပ်တာ ကို Truths Table ကို ကြည့်ရင် သိနိုင်ပါတယ်။ 

Dependent Events ဆို And 

output Event တစ်ခု ဖြစ်လာဖို့အတွက် Input events နှစ်ခု ရဲ့ Probability က 1 ဖြစ်မှသာ output ရဲ့ event က 1 ဖြစ်မှာ ဖြစ်ပြီး event တစ်ခုက 0 ဖြစ်တာနဲ့ output ရဲ့ event က 0 ဖြစ်ပါတယ်။ ဒါက 0 နဲ့ ဘာ နဲ့ မြှောက်မြှောက် 0 ရတဲ့ Multiplication Rule ကို အသုံးပြုထားတာ ဖြစ်ပါတယ်။ 

Input A	Input B	Output
0	0	0
0	1	0
1	0	0
1	1	1

Example အနေနဲ့ ပြောရရင် သင်က သင့် Crush နဲ့ ရည်းစား ဖြစ်ချင်တယ်ဆိုရင် သင်ကလည်း ဖွင့်ပြောရမှာ ဖြစ်သလို သူကလည်း လက်ခံမှ ရမှာပါ။ သင်ဖွင့်ပြောသည် ဖြစ်စေ ၊ မပြောသည် ဖြစ်စေ သူဘက်က လက်မခံ ဘူးဆိုတာနဲ့ သင်နဲ့ သင့် Crush ရည်းစား ဖြစ်လာမှာ မဟုတ်ပါ။ 

Independent Events ဆို Or 

output Event တစ်ခု ဖြစ်လာဖို့အတွက် Input events နှစ်ခု ထဲက တစ်ခုရဲ့ Probability က 1 ဖြစ်တာနဲ့ output ရဲ့ event က 1 ဖြစ်မှာ ဖြစ်ပြီး event နှစ်ခုလုံးက 0 ဖြစ်မှသာ output ရဲ့ event က 0 ဖြစ်ပါတယ်။ ဒါက 0 နဲ့ ဘာ နဲ့ ပေါင်းပေါင်း ပေါင်းတဲ့ Number ရတဲ့ Addition Rule ကို အသုံးပြုထားတာ ဖြစ်ပါတယ်။

Input A	Input B	Output
0	0	0
0	1	1
1	0	1
1	1	1

example ပြောရရင် သူငယ်ချင်း နှစ်ယောက် ရှိတယ် ဆိုပါဆို့။ နှစ်ယောက်ထဲက တစ်ယောက်က အသည်းကွဲတာနဲ့ ကျန်တစ်ယောက်က ကွဲသည် ဖြစ်စေ ၊ မကွဲသည် ဖြစ်စေ အရက်ဆိုင်ရောက်သွားမှာပဲ ဖြစ်ပါတယ်။ 

And ကို ပြောင်းပြန် NAND ( Not And ) 

NAND ဆိုတာက And ရဲ့ reverse ဖြစ်ပါတယ်။ ဆိုလိုချင်တာက AND gate ရဲ့ Output ကို ပြောင်းပြန် ယူရတာ ဖြစ်ပါတယ်။ 

Input A	Input B	Output	NAND
0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	0

Or  ကို ပြောင်းပြန် NOR ( Not OR ) 

NOR ဆိုတာက OR ရဲ့ reverse ဖြစ်ပါတယ်။ ဆိုလိုချင်တာက OR gate နဲ့ operation ရဲ့ Output ကို ပြောင်းပြန် ယူရတာ ဖြစ်ပါတယ်။ 

Input A	Input B	Output	NOR
0	0	0	1
0	1	1	0
1	0	1	0
1	1	1	0

Input ပြောင်းပြန် NOT 

Not Operator ရဲ့ Concept ကတော့ output က  input ရဲ့ ပြောင်းပြန် ဖြစ်ပါတယ်။ 

Input	Output
0	1
1	0